
全国トップクラスの難易度でも知られています。
……私の出身校なので自分で言うのも恥ずかしいですが。
灘中の入試は2日に渡り開催され、その両方の合計点で合否が決定します。
なお、算数は1日目、2日目の2回の試験があります。
今回、灘卒の筆者が2023年灘中算数1日目を解いてみました。
(灘卒と言っても高校からの入学なのですが……(灘では新高と言います))。
受験のプロではない一般的な灘卒の人間が解いた解き方と所要時間、感想を書いていきます。
今後、灘中受験を検討する方に参考にしていただければ幸いです。
灘を全く考えていない大人でも、クイズ感覚で解いてみてはいかがでしょうか?

(塾無しで灘に合格し、現役で東大理3に進学した同級生はZ会を使っていました。)
(注意)
ブログの性質上作図が難しいため、図形問題は作図無しで考え方だけ書いておきます。
問題文は、以下よりダウンロードお願いします。
灘中学より著作権上、当ブログでの過去問の掲載に問題ないと許可を頂いたため、今日と明日で1日目と2日目の解説をアップします。
母校とはいえ、寛容な処置に感謝します。
(問い合わせの際にビビってしまい、卒業年と実名を伝えて許可を貰ったのですが……。)
灘中算数 2023年 1日目
大問1

この問題はふたつのポイントがあります。
①西暦の素因数分解
②1/14-1/15の計算(分数は/を用いて表記しています。1/14は14分の1という意味です)
①2023=7×17×17
灘に限らず、受験年(西暦)を計算問題に含むことは非常に多いため、受験年の素因数分解は受験前から知っておいても損は無いと思います。
(来年であれば2024=2×2×2×11×23)
②1/14-1/15=(15-14)/(15×14)
これは中学受験頻出の分数計算(例えば、1/2+1/6=1-1/2+1/2-1/3=2/3)を知っていればすぐ思いつきます。
結果として、式の左辺は2023を17で2回割った商である7に1/(15×14)をかけるので、暗算でも1/30と分かります。
右辺でこれに当てはまるのは□が51のときです。
この問題は、暗算で1分かからず解けるかなと思われます。

大問2

三点が三角形にならない場合とは、直線に並ぶときです。
図の中で直線はAB、BC、CA、DE、EF、FDの6本です。
それぞれで3点の選び方は、4×3×2÷(3×2×1)=4 (4点中3点の選び方、選ばれない1点の選び方と考えて4通りでも良い)
それが6本あるため、4×6=24通り。
この問題も、暗算で1分かからないで解ける問題だと思います。

大問3

二つの計算を筆算で書くと、次のようになります。
DEF ABC
BC DE
+ A + F
左右の筆算を比べていきます。
それぞれの赤字の部分が同じであることに注目します。
1の位で、CとFが共通であるため、A=Eと分かります。
A=Eであるため、1の位の数字は全て一致していることになります。
次に10の位で、1の位から繰り上がってくる数字ならびにBが共通であるため、D=Eと分かります。
つまり1の位だけでなく、10の位も全て一致している事が分かります。
次に100の位で、10の位から繰り上がってくる数字が共通であることから、A=Dと分かります。
つまり、答えは(選択肢の)ウ、エ、スです。
問題だけを見て解き方が思い浮かばなくても、筆算を実際に書いてみることで思いつくことができます。
所要時間としては3分程度だと思われます。

大問4

数字は1つのグループに4個ずつ含まれるため、2023番目のグループまでに8092個の数字が出てくることになります。
つまり、2023番目のグループには8089番目の数字から8092番目の数字が含まれます。
この数列は1から9までの数字が繰り返されているため、この9個の数字を1組とすると、8092番目の数字までに
8092÷9=899余り1
となり、8092番目の数字は1と分かります。
(2022番目のグループまでに含まれる8088を9で割って考えても良い。)
よって2023番目のグループの数字は最後からさかのぼると1、9、8、7の4つになるため、合計は25です。
また、8092番目の数字までに1から9の数字の組み合わせが899組あり、8092番目の数字は1であるため、数字の合計は
(1+9)×9÷2×899+1=40456 となります。
↑ 1から9までの数字の和
一つの数列に二つの規則が含まれる問題ですが、一つ一つは基本的な内容だと思います。
(二つの規則:1から9までの9個の数字が繰り返されること、4個の数字を1つのグループと考えること)
所要時間は3-4分程度と思われます。

大問5

Aの選び方は6×5÷2=15通り。
Bの選び方は4×3÷2=6通り。
Cは残り1通り(2×1÷2=1通り)。
よって並べ方は全部で15×6×1=90通り。
このうちAの大きい数がBの大きい数より大きい場合と小さい場合は同じと考えられる(同様に確からしい)。
このため、答えは90÷2=45通り。
場合の数の問題としては、標準的な問題かなと思います。
所要時間としては1分程度と思われます。

大問6

不完全なグラフの意味が一見分かりにくい問題ですが、それぞれのポイントとなるタイミングで何が起こっているのか整理すると容易です。
まず2か所あるy=0は、AさんとBさんがすれ違ったことを表します。
また、y=1250は二人の距離がそれ以上広がらなくなり、それ以降近づくことを表します。
それは、AさんもしくはBさんの早い方(まだどちらかは不明)が折り返したことを意味します。
x=30以降、二人の距離が大幅に縮まるため、ここで二人とも折り返し互いが近づき始めることが分かります。(遅い方が折り返し点に到着。)
グラフの最後、y=1000がこの問題のポイントです。
グラフだけで意味が分かりにくいため、もう一度問題文を読んでみましょう。
この問題は、AさんがPに到着するまでのグラフです。
つまり、この時にAさんがPに到着し、Bさんは歩いている最中と分かります。
(Aさんの方がBさんより早い。)
ここまでをもう一度整理すると、AさんがPQ間(片道)を歩く間にBさんは1250m歩いています。
さらにAさんがPQ間を往復する間にBさんはPQ間の片道+1000mを歩いています。
このことから、AさんがPQ間の片道を歩く間にBさんが歩いた距離との差が250m広がることが分かります。
AさんがPQ間を1回歩いた状態でBさんは1250m歩いているので、0回の時点では1500mの距離が開いている、つまりPQ間の距離は1500mと分かります。
1回250mずつ差が広がるため、1250÷250=5回 BさんがPQ(片道)を歩く間に、Aさんは6回歩く、つまり速さの比が6:5と考える考え方もあります。
その場合、Bさんが1250m歩く間にAさんがPQ間を歩くので、1250÷5×6=1500mです。
また、Bさんは30分でPQ間を歩くため、二人で歩く場合はかかる時間は5/11倍(BさんとAさん+Bさんの速さの比は5:11、かかる時間の比は11:5なので)。
よって最初に出会うのは30×5/11=150/11分後。
この問題は一見難しそうですが、条件を整理すればそれ程難しくないかなと思います。
所要時間は5分ほどと思います。

大問7

はじめ、5760円(1ナダ150円)
1日目終了時、2880円+24ナダ(1ナダ120円)
2日目終了時、1440円+40ナダ(1ナダ90円)
4日目終了時、5940円+?ナダ(1ナダ180円)
ナダが高くなる場合を「高」、安くなる場合を「安」と表記し、3日目、4日目のナダの変動が(高、高)、(高、安)、(安、高)の3通りを考えます。
((安、安)では2日目から4日目に円が増えないため、この問題と矛盾します。)
(高、高)の場合
ナダは3日目20ナダ、4日目10ナダになります。
4日目に10ナダを1ナダ180円で円に替えるため、4日目に1800円増えます。
つまり、3日目に5940-1800=4140円持っていました。
20ナダを円に替えたことで4140-1440=2700円増えているので、1ナダ2700÷20=135円。
(高、安)の場合
ナダは3日目に20ナダ減り、20ナダになります。
4日目に円が半分になって5940円になっているので、3日目には5940×2=11880円ありました。
このとき2日目(1440円)から11880-1440=10440円増えたことになります。
20ナダを10440円と替えているので、10440÷20=522円。
(安、高)の場合
3日目に円は720円になり、720円をナダに替えたことになります。
4日目に5940円になっているので、5940-720=5220円増えています。
このとき1ナダが180円なので、5220÷180=29ナダ替えていることが分かります。
3日目、58ナダあったことが分かり、2日目から18ナダ増えています。
このとき720円を18ナダと替えているため、720÷18=40円。
これらから答えは最も高い場合で522円、最も安い場合で40円です。
条件を落ち着いて整理するとそれほど難しくありませんが、限られた時間内に3通りの場合を落ち着いて考えるのがやや難しいように思います。
所要時間は5-6分程度でした。

大問8
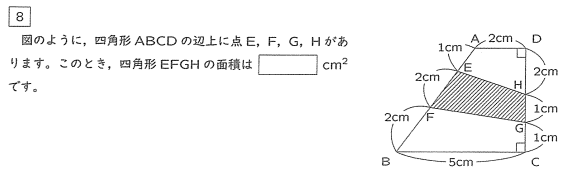
AH、HF、FC、HBに補助線を引きます。
四角形EGFHは、三角形EFHと三角形FGHに分けられます。
三角形EFHは三角形AHBの2/5です(辺ABを底辺と考える)。
三角形AHBは四角形ABCDから三角形AHDと三角形BCHを除いた部分なので
(2+5)×4÷2ー2×2÷2-5×2÷2=7
よって三角形EFHは7×2÷5=2.8
また、FからCDに下ろした垂線の長さは2+3×3/5=3.8です。
(AからBCに垂線を下ろし、その直角三角形との相似を利用してFからCDに下ろした垂線の長さを求めます)
よって、三角形FGHの面積は1×3.8÷2=1.9
合計すると、EFGHの面積は4.7となります。
他の求め方でも出せますが、きれいな求め方は思い浮かびませんでした。
泥臭く一つ一つ求めても、所要時間は5分程度と思います。

大問9

この問題のように、同じ大きさの円を円周がもう一方の円の中心を通るように描くと、重なる部分の上下に正三角形を2個作ることができます。
(全ての辺の長さが円の半径と等しい(同じである)ため正三角形になる)
よって円周の重なる部分(この問題でカウントしない部分)は、中心角120度のおうぎ形の弧と等しくなります。
これが12か所(重なりは6か所×2(左右の円))あるため、円4個分の円周と等しくなります。
よって求める部分は円3個分(7-4)になるので、
2×3.14×3=18.84
となります。
重なり自体は比較的簡単に思い浮かぶと思われます。
所要時間は2-3分程度と思います。

大問10

先に言うと、私はこの問題はできませんでした。
解き方を聞くとなるほどと思う良問だと思います。
点Eから辺BC、辺AD、辺ABに垂線を下ろし、交点をそれぞれJ、K、Lとします。
三角形EJCと三角形EKIは合同です。
また、三角形EJBと三角形ELFも合同です。
よって、四角形AFEIと三角形BCEの合計は三角形EJC+三角形EKI+四角形ALEKです。
ここで四角形ALEKは、三角形EJCが2つ重なった形であるため、三角形EJC4個分で56cm2となっていることが分かります。
この三角形4個を正方形GHIEの外側に並べてできる正方形の面積は121、つまり1辺の長さは11cm。
正方形CHIEの内側に並べた余りの正方形の面積は9、つまり1辺の長さは3cm。
つまりJC+EJ=11、JC-EJ=3なのでJC=7、EJ=4です。
四角形BEFGは三角形EJB4個分なので、4×4÷2×4=32cm2となります。
この問題は私は思い浮かびませんでしたが、56cm2の部分がどういう誘導になっているかを思いつくかどうかかなと思いました。
他の問題が比較的容易なため、見直しをして余った時間をつぎ込んでも良いのかなと思います。
大問11

この問題は左のNの形と右の三角形に分けて考えました。
Nの形は(重心が回転した長さ×面積)で求めることができます。
(パップス・ギュルダンの定理。小学生の頃の私は知らなかった気がします)
Nの部分の体積は7×3.14×16
右の三角の部分の体積は、大きい円錐から小さい円錐と円柱を引くように考えて
(9×9×15÷3-6×6×10÷3-6×6×5)×3.14
合計すると217×3.14=681.38
この問題は、パップス・ギュルダンの定理を使わなくても解けますが、少し面倒くさい問題かなという印象です。
所要時間は5-7分程度と思います。
大問12

ABCを通る切り口は正六角形になります。
各段に並ぶ立方体の図に切り口がどこを通るか書き込むと容易です。
1、3、5段目の切り口は左の図に、2、4、6段目の切り口は右の図に書き込みます。
切り口に正方形の半分の三角形が何個あるか数えていきます。
(実際には立体なので長さが変わり、正三角形になる)
赤は15個、白は24個あるため、答えは5/8となります。
切り口の三角形を数えるだけの問題です。
所要時間は、作図や数える時間併せて5分強といったところだと思います。
最後に
中学入試は年々難しくなっていると言う人がいます。
ただ、2023年の1日目は私が受験した約30年前と比較しても、それほど難しくなかった気がします。
おそらく灘を受験するような生徒は10問前後は正解するのではないでしょうか。
限られた時間でケアレスミスをせず解くという、プレッシャーがかかるテストだと思います。
今後受験される方は頑張って対策してください。



